Employees of the Laboratory of Theoretical Physics JINR have derived the most general formulas that make it possible to obtain multi-loop renormalization group equations in an arbitrary generalisation of the Standard Model without the need for explicit calculation of millions of Feynman diagrams arising in the higher orders of perturbation theory.

Thanks to LHC, it is known that the Standard Model of elementary particles describes a huge number of processes at the energy scales available for modern accelerators. The Standard Model (SM) covers eighteen parameters describing the interactions of fermions (quarks and leptons), vector (photon, W/Z bosons) and scalar (Higgs) bosons. For example, the “coupling ” of the strong interaction, which determines the effective quark-antiquark interaction force, is among them. Alternatively, a well-known electromagnetic coupling that is associated with an electric charge. By defining them, or better to say measuring them, it is possible to make predictions.

However, scientists have been looking for signs of new physics beyond the Standard Model for many years. Theorists are trying to make generalisations of the SM, while experimenters are trying to find traces of new particles and identify new interactions.

If scientists extend the SM, then they add new parameters. For example, the existence of a heavier analogue of the Z boson, which interaction with other particles is determined by a new gauge “coupling” (commonly identified as g) could be assumed. They can also add several Higgs bosons, which interaction with each other, as well as with quarks and leptons, will be determined by “self-couplings” (λ) and Yukawa “couplings” (y) respectively.

“It is often important to understand what happens to the model if we try to extrapolate it to the region of high energies, not available for modern (and possible even future) accelerators. On the contrary, by defining a new model of New physics at a very high energy scale (it is usually assumed that in this case the model has greater symmetry than the SM), it is interesting to understand what deviations from the SM predictions could be measured in experiments,” said Alexander Bednyakov, Head of the BLTP JINR Department of Quantum Field Theory, one of the authors of the paper.

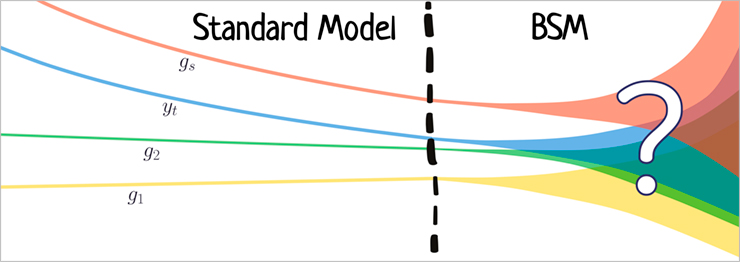Fig. 1. Scale dependence of couplings: from the Standard Model to possible physics beyond the Standard Model (BSM)

“Renormalization group equations show how, thanks to virtual particles, charges are screened or anti-screened when the energy scale changes (μ). Such effects have a universal nature, and we are trying to consider them in our calculations. Each new loop corresponds to the production and absorption of some virtual particle. The more complex the model, the more different options we have,” Alexander explained. He added that in order to find the dependence of the “charges” on the scale in a particular model, it is necessary to carry out time-consuming calculations of Feynman diagrams.

The complex calculations performed during the course of the work were transformed into formulas, which are quite simple differential equations. After defining parameter values (interaction force) at one scale, it is possible to find their values at another scale. Fig. 2 schematically shows the most general renormalization group equations for gauge, Yukawa couplings, as well as scalar self couplings, obtained in a series of scientific papers. It can be seen that the number of terms in the formulas increases with the order of the perturbation theory. Each term can be represented in the form of a Feynman diagram, in which solid lines correspond to fermions, wavy lines correspond to gauge bosons, and dotted lines correspond to scalar particles.

Fig. 2. General renormalization group equations for gauge, Yukawa couplings, and scalar self couplings

Prepared equations are convenient because all calculations of complex integrals relevant to diagrams have already been carried out. It is enough just to define a model, i.e. list all the particles and write out the Lagrangian function describing their quantum numbers and interactions.

Non-specialists in loop calculations can use these equations as well. For example, theoretical physicists can use them to analyse New physics. In addition, these prepared formulas are used in condensed matter physics – in the theory of phase transitions of the second kind for calculating various critical indices. This result was highlighted as one of the brightest obtained at BLTP JINR in 2021. The authors of a series of scientific papers devoted to this topic are Alexander Bednyakov and Andrey Pikelner. They received the First JINR Prize for 2021 in the section “For Theoretical Physics Research”.

“Another important result of the series is closely related to quantum chromodynamics (QCD), which describes quarks, gluons, and their interactions. We believe that quantum chromodynamics should work at both high and low energies,” Alexander continued. At large distances, the interaction between quarks becomes so strong that the use of standard perturbation theory is difficult. Computer calculations on a discrete Euclidean space-time lattice can help. In particular, the High Precision QCD (Quantum chromodynamics) collaboration carries out such calculations. It includes theoretical physicists from scientific centres in America, England, Italy, Japan, Spain. Among other things, they extract from the lattice data the key parameters of QCD, such as the quark mass and the strong interaction constant.

“It is possible to take the quark mass or the strong interaction coupling measured at high energies and compare it to what is extracted on the lattice. If the values are similar, it means that quantum chromodynamics “works”. If they are not similar, there is a question then: is it necessary to modify the model or just improve the accuracy of theoretical calculations. It is often high accuracy that allows specialists to find small deviations — possible signs of New physics,” the researcher explained. An important nuance here is that the value extracted from the lattice data can often not be directly compared to a similar one, but used in high-energy physics. This arbitrariness is “embedded” in the theory of renormalization, but we can control it within the framework of perturbation theory. It is precisely this kind of recalculation formulas that we have found in the three-loop approximation. We are very pleased that the HPQCD collaboration immediately used our calculations for a new record of accuracy in determining the mass of an enchanted quark,” Alexander Bednyakov concluded.

The scientists present themselves the key results of the scientific paper.

A new era of RG calculations at BLTP: modern methods, tools, and recent achievements

The renormalization group (RG) method allows specialists to systematically improve the accuracy of calculations in perturbation theory. The key objects of the method are the renormalization group functions, which specify the response of various quantities to a scale variation. Their calculation is a separate task and turns out to be one of the most time-consuming and technically complex parts of an RG analysis.

The presented series of papers covers the discussion of various aspects of multi-loop calculations, as well as the recent achievements related to the generalisation of the state-of-the-art record results in the SM and φ4 in case of arbitrary quantum field models.

In the framework of the most general renormalizable theory in four dimensions, for the first time we derive the expressions for the beta functions of gauge and Yukawa couplings at four and three loops respectively [1]. The originality of the utilized approach in the fact that we bypass tedious and cumbersome calculations by considering simple toy models and fixing unknown model-independent coefficients in general expressions for the RG functions using them. Thanks to our results, it became possible to carry out precision RG analysis of an arbitrary New Physics model without the need for explicit diagrammatic calculation and renormalization. As an application of the developed formulas, we derived the four-loop beta functions of all gauge couplings in the SM and its generalization with several Higgs doublets. In addition, for the first time, six-loop expressions have been obtained for the RG functions of both dimensionless and dimensional parameters of the most general φ4 model [2]. One of the possible applications of this result is the study of various classes of universality in the theory of critical behaviour corresponding to different symmetries and different order parameters.

Calculations within the framework of specific physical models were an important step towards the indicated results. In particular, the computation of the four-loop electroweak contributions to the beta function of the strong coupling in the SM [3] had a significant impact on further research. Thanks to a careful analysis of the uncertainties arising from a naive approach to dimensional regularization of chiral theories, we obtain a result, which was subsequently confirmed by an independent calculation and further generalized in case of an arbitrary field theory [Poole & Thomsen (2019)]. We also considered the scalar sector of simple SM extension with an additional Higgs doublet [4] and found the corresponding RG functions at the three-loop level. As a by-product of the calculation, we corrected a typo in the well-known papers of the 1980s, which were widely used in computer codes for the analysis of New Physics.

Another important result is the derivation of three-loop formulas that make it possible to relate the results of nonperturbative lattice calculations with the key QCD parameters (strong coupling [5] and quark masses [6]) used in calculations of observables for collider experiments. For this purpose, we use original ideas to perform sophisticated analytical calculations of the three-loop vertex functions [7] in symmetric kinematics. It is worth mentioning the fact that the obtained result [6] was immediately used by the HPQCD collaboration to improve the accuracy of the lattice determination of the charmed quark mass.

Modern calculations at high orders can not be carried out without computers and the use of new approaches and algorithms for calculating Feynman diagrams. In the papers of the series, an optimised publicly available code was developed for the computation of four-loop vacuum diagrams [8]. It allowed subsequently carrying out a non-trivial calculation of counterterms for all five-loop diagrams necessary for the derivation of RG functions of scalar models in six dimensions [9], thereby opening up new possibilities for RG analysis in higher dimensions.

It should also be noted that the peculiarity of the presented series of papers is that the provided results are in demand in different areas of modern physics. We managed to go beyond the standard approaches and develop a necessary set of tools that allows non-specialists in multi-loop calculations to use the renormalization group method to obtain important physical results.

The Bogoliubov Laboratory of Theoretical Physics has a long and rich history of such calculations. Starting with the fundamental scientific papers of N. N. Bogoliubov and D. V. Shirkov, the RG method and related multi-loop calculations of Feynman diagrams have been used at JINR to obtain many interesting results during past years. Among them are well-known calculations in scalar φ4 and quantum chromodynamics (QCD). As for the Standard Model (SM), the recent computation of three-loop RG functions caused a great resonance in the literature. After measuring the mass of the Higgs boson in 2012, these results allowed specialists to carry out the most complete and self-consistent vacuum-stability analysis, which led to heated discussions on possible instability of the SM and a need for New Physics.

Literature:

[1] Alexander Bednyakov и Andrey Pikelner. Four-Loop Gauge and Three- Loop Yukawa Beta Functions in a General Renormalizable Theory . в: Phys. Rev. Lett. 127.4 (2021), с. 041801. doi: 10 . 1103 / PhysRevLett . 127.041801. arXiv: 2105.09918 [hep-ph].
[2] A. Bednyakov и A. Pikelner. Six-loop beta functions in general scalar theory . в: JHEP 04 (2021), с. 233. doi: 10 . 1007 / JHEP04(2021 ) 233. arXiv: 2102.12832 [hep-ph].
[3] A. V. Bednyakov и A. F. Pikelner. Four-loop strong coupling beta-function in the Standard Model. в: Phys. Lett. B 762 (2016), с. 151 156. doi: 10.1016/j.physletb.2016.09.007. arXiv: 1508.02680 [hep-ph].
[4] A. V. Bednyakov. On three-loop RGE for the Higgs sector of 2HDM . в: JHEP 11 (2018), с. 154. doi: 10.1007/JHEP11(2018)154. arXiv: 1809. 04527 [hep-ph].
[5] A. Bednyakov и A Pikelner. Four-loop QCD MOM beta functions from the three-loop vertices at the symmetric point . в: Phys. Rev. D 101.7 (2020), с. 071502. doi: 10 . 1103 / PhysRevD. 101 . 071502. arXiv: 2002 . 02875 [hep-ph].
[6] Alexander Bednyakov и Andrey Pikelner. Quark masses: N3LO bridge from RI/SMOM to MS scheme . в: Phys. Rev. D 101.9 (2020), с. 091501. doi: 10.1103/PhysRevD.101.091501. arXiv: 2002.12758 [hep-ph].
[7] Andrey Pikelner. Three-loop vertex integrals at symmetric point . в: JHEP 06 (2021), с. 083. doi: 10. 1007/ JHEP06(2021) 083. arXiv: 2104. 06958 [hep-ph].
[8] Andrey Pikelner. FMFT: Fully Massive Four-loop Tadpoles . в: Comput. Phys. Commun. 224
(2018), с. 282 287. doi: 10.1016/j.cpc.2017.11. 017. arXiv: 1707.01710 [hep-ph].
[9] Mikhail Kompaniets и Andrey Pikelner. Critical exponents from ve-loop scalar theory renormalization near six-dimensions . в: Phys. Lett. B 817 (2021), с. 136331. doi: 10.1016/j.physletb.2021.136331. arXiv: 2101. 10018 [hep-th].