Theoretical physics helps to make weather forecasts more accurate
News, 24 October 2022
At the Laboratory of Theoretical Physics JINR, studies of turbulent motions in liquids and gases are carried out. These studies enable us to reveal the laws that govern many natural phenomena. Making more accurate weather forecasts, calculating the trajectory of industrial emissions and gaining a deeper understanding of many other processes is possible with the use of stochastic equations.
Flows in liquids and gases are of two main types: turbulent-chaotic and vortex-and laminar moving in layers without mixing. The motions of the second type are ordered and their trajectory is easy to determine, whereas in the case of turbulent flows the physical picture is more complicated. The positions and amounts of particles in such the turbulent environment, after a while, can be predicted only approximately. Scientists acknowledge that a complete theory of turbulence is incredibly difficult to construct; nevertheless, over the past quarter of a century, the scientific community has made progress in understanding these processes.
Turbulence describes a whole class of phenomena in the atmosphere and hydrosphere of our planet: winds and sea currents, waves, tornadoes and tsunamis, the drift of garbage patches in the oceans, etc. Even blood can flow through the veins both laminar (usually under conditions of physiological rest) and turbulent, with a narrowing or expansion of a blood vessel, a change in blood viscosity, and also with the formation of plaques in an artery or vein.
“There are practically no completely laminar flows in nature, they are more common in viscous liquids, Deputy Director of the Laboratory of Theoretical Physics, Doctor of Physical and Mathematical Sciences, Professor Michal Hnatič commented. Viscosity gives the flow a “braking force”, creates internal friction. The greater the viscosity of the system, the more energy must be pumped to generate vortices in it. Such a motion has always a tendency to break loose: to become turbulent, chaotic.
Therefore, in principle, it is not possible to predict the weather exactly, in all details, even with the most modern computers that calculate the direction and speed of air currents. Weather forecasts are most accurate when the weather is calm as long as the air flow is close to laminar. Then, for example, we can say that good warm weather will last five days – in this case, there are almost no mistakes. As soon as sufficiently strong pressure drops occur on the outskirts of the atmospheric front, the air begins to turbulize, and eddies of all sizes ultimately emerge.
Turbulence has a tremendous impact on the transport of impurities in the oceans, seas, or air, for example, on the spread of smoke from a chimney in a thermal power plant or a factory. Scientists can track how the smoke flies, but at the same time, give only average characteristic: what average size of a cloud will be over a given period of time. “In this case, a cloud will have a complex form, but we can say that if we imagined it as some average ball, then it would have a diameter of, for example, three kilometers. We can also determine the average propagation speed of this cloud”, Michal Hnatič said.
These studies make it possible to find out what the average concentration of substances in a turbulent flow will be at a certain distance from the chimney. This gives an understanding of how far you need to locate a residential area from an industrial object and how high the chimney should be so that the smoke does not descend on the city.
“Transport of particles is a very complicated phenomenon. There are various equations that describe the movement of an object in space and time. Many of them describe the trajectory unambiguously, as in the case, for example, when shooting from a rifle: aiming from one point you hit a certain target, aiming a little higher – you hit another higher one. This movement can be controlled. In turbulence, it is impossible to control anything – instability arises, errors accumulate – the so-called butterfly effect appears. There are equations that describe this uncontrollability, but the problem is that their solutions are unstable. They allow one to derive only certain average characteristics, evaluate correlations in the system”, Michal Hnatič explained.
A cycle of articles on the phenomenon of turbulence in liquids and gases “Calculation of critical exponents and representative physical parameters of scaling behavior of stochastic systems by quantum field theory methods” by a group of authors: Loran Adzhemyan, Nikolai Antonov, Michal Hnatič, Juha Honkonen, Polina Kakin, Georgii Kalagov, Mikhail Kompaniets, Tomáš Lučivjanský, Lukáš Mižišin, Mikhail Nalimov representing the research centres: BLTP JINR, St. Petersburg State University, P. J. Shafarik University and IEF SAN, Košice (Slovakia), University of Helsinki and National Defense University, Helsinki (Finland), was awarded the 2021 first JINR Prize in the nomination “For Theoretical Physics Research”. This cycle includes works published by the team over the past 25 years.
Using the methods of quantum field theory, the team of scientists studied classical systems of turbulence and achieved novel outcomes: the energy spectrum was calculated and the existence of intermittency or fractality was explained. It was proved that turbulence as if “flickers” and there are islands of laminarity in it, which disappear in one place and appear in another. The alternation of such laminar areas with chaos is called intermittency or fractality (multifractality).
One more striking result is the study of the dependence of the rate of chemical reactions in a complex turbulent medium.
“We have derived governing equations that can be solved and thus predict the dependence of the concentration of reactive particles per unit volume and time. Over time, these particles, when colliding, cease to be active, form a chemically inert molecule that no longer participates in the reaction. The rate of precipitation of molecules or a decrease in the concentration of these chemically active particles depends on the medium in which the process takes place. This is also of great practical importance. Poisonous substances emitted with smoke from the chimney can be neutralised over time. So the chaotic process helps speed up the disappearance of chemically active particles”, Michal Hnatič said.
 Example of turbulence obtained experimentally
Example of turbulence obtained experimentally
About the main results of the studies
Theoretical understanding of turbulence is one the most important unsolved problems in classical physics. Of course, the concept of turbulence encompasses a wide class of physical phenomena of various nature, so that any exhaustive and completed “theory of turbulence” can hardly ever be constructed. However, there is a “canonical list” the of problems: existence and stability of solutions to the hydrodynamics equations, convective (thermally driven) turbulence, instability of laminar flows, decaying turbulence, etc., which have both practical and conceptual significance and have always been in the focus of theorists’ attention. One of them is the problem of describing the fully developed (homogeneous, isotropic) hydrodynamic turbulence (in particular, its inertial-range behaviour).
Turbulent flows occurring in various liquids or gases at very high Reynolds numbers exhibit a number of general encouraging phenomena and features (cascades of energy and other conserved quantities, scaling behaviour with apparently universal “anomalous exponents,” etc.), indicating that the developed turbulence can be described within the framework of a certain self-sufficient and internally consistent theory. The most notable feature of developed turbulence, which does not fit into the framework of the classical phenomenological Kolmogorov-Obukhov theory, is the “intermittency” phenomenon arising due to the strong energy flux fluctuations. In particular, it manifests itself in a singular dependence, presumably power-law, of various equal-time correlation and structure functions, on the distances and the integral scale, and is characterised by an infinite number of independent anomalous exponents (anomalous multi- scaling). Both experiments and numerical simulations show that the anomalous scaling is more strongly pronounced for the passive turbulent transfer of scalar and vector fields (temperature, impurity concentration, magnetic field) than that for the velocity field itself. Therefore, the problem of passive transfer is an essential integral part of the study of scaling in a turbulent medium.
A related class of problems is associated with the study of the role of turbulence in fluids near their critical points, at which the systems turn out to be extremely sensitive to external influences and hydrodynamic fluctuations, which ultimately lead to the emergence of new dynamic scaling universality classes both in classical and quantum systems, for example, in liquid helium. In the latter, vanishing of the viscosity coefficient immediately leads to arbitrarily large Reynolds numbers even at low flow rates.
Fluctuations of random velocity fields, including turbulent ones, affect many other stochastic processes in nature. Among them, a special place is occupied by chemical reactions proceeding in random environments, models of non-equilibrium critical behaviour, describing the roughening of a randomly growing surface (like the Kardar-Parisi-Zhang equation), models of directed percolation, describing the propagation of fronts of forest-fires, epidemics, the growth of tumours and bacterial colonies, and others. It turns out that taking into account the turbulent motion of the environment significantly enriches the universality classes of such systems.
It should be emphasised that the dynamical physical quantities (velocity, impurity concentration, magnetic field, etc.) are random fields and their evolution is described by nonlinear stochastic differential equations. The main goal of theoretical research is to find various averaged statistical characteristics of those fields: correlation functions, response functions, structure functions and more complex objects. Suitable methods for achieving these goals are the methods of quantum field theory (renormalization group) and non-equilibrium statistical physics. The authors have contributed significantly to the adaptation and improvement of these methods for solving turbulence problems. Original methods were developed to calculate the representative constants and parameters of turbulent systems using perturbation theory and the critical dimensions of the so-called “dangerous” composite operators forming a multi-fractal (intermittent) behaviour of statistical correlations of the investigated random fields.
Since the second half of the 90s of the last century, their use has led to several significant results in the theory of developed turbulence and the study of its influence on other stochastic processes in open systems. Below we briefly summarise the main results of the authors, published in leading international journals in 1995-2021, including four review articles [6, 14, 27, 35].
- Within the framework of dimensional-analytical regularization [1], the Kolmogorov constants and the skewness factor have been calculated, which are consistent with the experimental values [2]–[5]. The kinetic energy spectrum in the energy-containing and inertial interval and the transfer function in the energy balance equation, expressed in terms of the triple correlation function of the velocity field, have been found [7]. The calculated Kolmogorov constant Ck and the kinetic energy spectrum are in a good agreement with experimental data.
- The advection of scalar and vector impurities by a turbulent medium has been investigated. Up to the three-loop approximation, the critical dimensions of the “dangerous” composite operators have been calculated, which determine the anomalous (intermittent) behaviour of the concentration and magnetic field in the inertial range [15]–[20]. It has been found that anisotropy, mirror symmetry breaking, and compressibility of the medium do not destroy the stability of critical regimes, but contribute to the anomalous dimensions of the composite operators [21]–[30].
- A quantum-field model has been formulated that describes the kinetics of the autocatalytic annihilation reaction in the presence of fluctuations of the density and velocity field.
- In [44]–[51] systematical investigation has been carried out of the influence of the motion of a medium (including turbulent one) on the scaling behaviour of a number of models of random growth of surfaces (interfaces between media, smoke, and flame fronts, landscapes the Kardar-Parisi-Zang models [44, 47] and Pastor-Satorras-Rotman [45, 46] and their modifications) and stochastic models of self-organized criticality (the Hwa-Kardar model [49, 50] and its variants). In all cases, possible types of scaling behaviour (“universality classes”) and regions of their stability have been found. The corresponding critical dimensions have been calculated in the leading orders of the renormalization group expansions, and in some cases, exactly.
- The influence of turbulent fluctuations on the phase transition to the superfluid state of Helium described in the framework of the models of critical dynamics has been analysed. A new critical mode has been established, and it has been shown that the developed turbulent fluctuations that appear due to the vanishing viscosity suppress the phase transition to a superfluid state. They affect the stability of previously known fixed points, at one of which, as is commonly believed, the phase transition takes place [52]–[56]. Analysis, which takes into account compressible infrared-relevant hydrodynamic modes, supports the generalised “model A” proposed on the basis of quantum kinetic theory in which the fixed point is unique [57, 58].
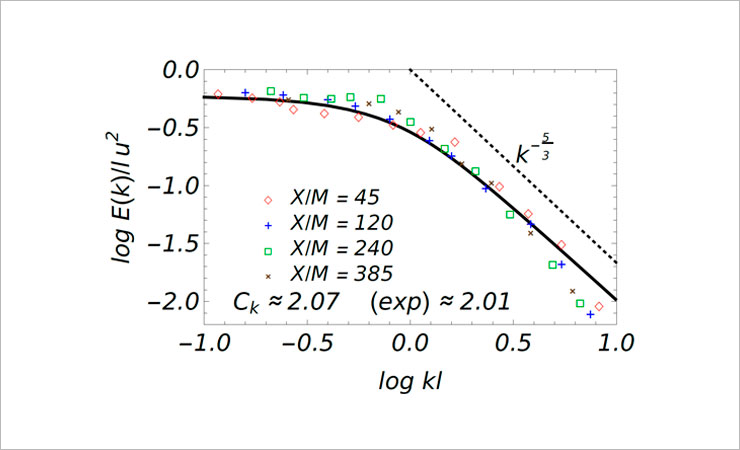 Longitudinal spectrum of energy as a wave number function (see [7] for details).
Longitudinal spectrum of energy as a wave number function (see [7] for details).
The leading correction to the Kolmogorov spectrum due to compressibility (second order in the Mach number) and anisotropic corrections to the Kolmogorov constant have been calculated. The validity of the Second Kolmogorov hypothesis for the energy spectrum has been justified, based on the assumption of isotropisation of the flow in the inertial interval [8]–[12]. The values of the Prandtl number for a passive scalar impurity and the magnetic Prandtl number in the models of developed turbulence with broken mirror spatial parity symmetry have been calculated [13, 14].
The RG methods have been used to study the asymptotic behaviour of the particle density at large times near the critical dimension two, and it has been shown that arbitrarily small fluctuations of the velocity field dominate the density fluctuations, accelerating the process of annihilation of particles. Calculations have been carried out up to the two-loop order [31, 32, 33]. The influence of sources and sinks simulating the interaction of active particles with a chemically active medium (chemical radicals) has been studied, and the corresponding actions have been constructed [34]. An integro-differential nonlinear equation for the mean particle density has been obtained, which is a generalization of the well-known kinetic equation in the mean-field approximation [35, 36].
The influence of hydrodynamic fluctuations on the processes of directed percolation has been investigated. New scaling regimes have been established; the critical exponents, that determine the temporal asymptotics of the average number of active agents, the survival probability of active clusters, and the effective radius, have been calculated [37]–[43].
References
[1] J. Honkonen, M. Yu. Nalimov, Z. Phys. B 99 (1996) 297
[2] L. Ts. Adzhemyan, N. V. Antonov, M. V. Kompaniets, A. N. Vasil’ev, Int. J. Mod. Phys. B, 17 (2003) 2137
[3] L. Ts. Adzhemyan, J. Honkonen, M. V. Kompaniets, A. N. Vasil’ev, Phys. Rev. E 68 (2003) 055302(R)
[4] L. Ts. Adzhemyan, J. Honkonen, M. V. Kompaniets, A. N. Vasil’ev, Phys. Rev. E 71 (2005) 036305
[5] L. Ts. Adzhemyan, M. Hnatich, J. Honkonen, Eur. Phys. J. B 73 (2010), 275
[6] M. Hnatich, J. Honkonen, T. Lučivjanský, Acta Physica Slovaca 66(2-3) (2016) 69
[7] L. Ts. Adzhemyan, M. Hnatich, D. Horvath, M. Stehlik, Phys. Rev. E 58 (1998) 44511
[8] L. Ts. Adzhemyan, M. Yu. Nalimov, M. M. Stepanova, Theor. Math. Phys. 104 (1995) 971
[9] D. Yu. Volchenkov, M. Yu. Nalimov, Theor. Math. Phys. 106 (1999) 375
[10] J. Buša, M. Hnatich, J. Honkonen, D. Horvath, Phys. Rev. E 55 (1997) 382
[11] N. V. Antonov, M. Hnatich, M. Yu. Nalimov, Phys. Rev. E 60 (1999) 4043
[12] J. Honkonen, Phys. Rev. E 104 (2021) 027101
[13] M. Hnatic, P. Zalom, Phys. Rev. E 94 (2016) 053113
[14] M. Hnatich J. Honkonen, T. Lučivjanský, Symmetry MDPI 11(10) 11(10) (2019) 1193
[15] L. Ts. Adzhemyan, N. V. Antonov, A. N. Vasil’ev, Phys. Rev. E 58 (1998), 1823
[16] L. Ts. Adzhemyan, N. V. Antonov, Phys. Rev. E 58 (1998), 7381
[17] N. V. Antonov, Phys. Rev. E 60 (1999), 6691
[18] N. V. Antonov, Physica D 144 (2000), 370
[19] L. Ts. Adzhemyan, N. V. Antonov, V. A. Barinov, Yu. S. Kabrits, A. N. Vasiliev, Phys. Rev. E 63 (2001), 025303(R)
[20] L. Ts. Adzhemyan, N. V. Antonov, V. A. Barinov, Yu. S. Kabrits, A. N. Vasiliev, Phys. Rev. E 64 (2001), 056306(R)
[21] L. Ts. Adzhemyan, N. V. Antonov, M. Hnatich, S. V. Novikov, Phys. Rev. E 63 (2001), 016309
[22] N. V. Antonov, J. Honkonen, Phys. Rev. E 63 (2001), 036302
[23] L. Ts. Adzhemyan, N. V. Antonov, A. V. Runov, Phys. Rev. E 64 (2001), 046310
[24] N. V. Antonov, J. Honkonen, Phys. Rev. E 66 (2002), 046105
4[25] L. Ts. Adzhemyan, N. V. Antonov, J. Honkonen, Phys. Rev. E 66 (2002), 036313
[26] N. V. Antonov, M. Hnatich, J. Honkonen M. Jurčišin, Phys. Rev. E 68 (2003), 046306
[27] N. V. Antonov, Journal of Physics A 39 (2006), 7825
[28] L. Ts. Adzhemyan, N. V. Antonov, P. B. Gold’in, M. V. Kompaniets, Journal of Physics A 46 (2013), 135002
[29] N. V. Antonov, M. Kostenko, Phys. Rev. E 92 (2015), 053013
[30] N. V. Antonov, N. M. Gulitskiy, M. M. Kostenko, T. Lucivjansky, Phys. Rev. E 95 (2017), 033120
[31] M. Hnatič, J. Honkonen, Phys. Rev. E 61 (2000), 3904
[32] M. Hnatič, J. Honkonen, T. Lučivjanský, Theor. Math. Phys. 169 (2011), 1489
[33] M. Hnatič, J. Honkonen, T. Lučivjanský, Theor. Math. Phys. 169 (2011), 1481
[34] M. Hnatič, J. Honkonen, T. Lučivjanský, Theor. Math. Phys. 176 (2013), 873
[35] M. Hnatič, J. Honkonen, T. Lučivjanský, Physics of Particles and Nuclei Letters 44 (2013), 316 – 348
[36] M. Hnatič, J. Honkonen, T. Lučivjanský, Eur. Phys. J. B 86 (2013), 214
[37] M. Dančo, M. Hnatič, T. Lučivjanský, L. Mižišin, Theor. Math. Phys. 176 (2013) 898
[38] N. V. Antonov, M. Hnatič, A. S. Kapustin, T. Lučivjanský, L. Mižišin, Phys. Rev. E 93 (2016) 012151
[39] N. V. Antonov, M. Hnatič, A. S. Kapustin, T. Lučivjanský, L. Mižišin, Theor. Math. Phys. 190(3) (2017) 323
[40] N. V. Antonov, M. Hnatič, A. S. Kapustin, T. Lučivjanský, L. Mižišin, Physics of Particles and Nuclei Letters 14(6) (2017) 944
[41] M. Hnatič, G. Kalagov, T. Lučivjanský, Eur. Phys. J. B 91 (2018), 269
[42] M. Hnatič, G. Kalagov, M. Yu. Nalimov, Nucl. Phys. B 926 (2018), 1
[43] S. Birnšteinov´a, M. Hnatič, T. Lučivjanský, L. Mižišin, V. Skult´ety, Theor. Math. Phys. 200(3) (2019) 1335
[44] N. V. Antonov, P. I. Kakin, Theor. Math. Phys. 185 (2015), 1391
[45] N. V. Antonov, P. I. Kakin, Theor.Math.Phys. 190 (2017), 193
[46] N. V. Antonov, P. I. Kakin, Journal of Physics A 50 (2017), 085002
[47] N. V. Antonov, P. I. Kakin, N. M. Lebedev, Journal of Physics A 52 (2019), 505002
[48] N. V. Antonov, P. I. Kakin, N. M. Lebedev, J. Stat. Phys. 178 (2020), 392
[49] N. V. Antonov, N. M.Gulitskiy, P. I. Kakin, G. E. Kochnev, Universe 6 (2020), 145
[50] N. V. Antonov, N. M. Gulitskiy, P. I. Kakin, V. D. Serov, Phys. Rev. E 103 (2021), 042106
[51] N. V. Antonov, M. M. Kostenko, J. Math. Sciences 257 (2021) 425
[52] M. V. Komarova, D. M. Krasnov, M. Yu. Nalimov, Theor. Math. Phys. 169 (2011) 1441
[53] M. Hnatich, M. V. Komarova, M. Yu. Nalimov, Theor. Math. Phys. 175 (2013) 781
[54] M. Dančo, M. Hnatič, M. V. Komarova, D. M. Krasnov, T. Lučivjanský, L. Mižišin, M. Yu. Nalimov, Theor. Math. Phys. 176 (2013) 888
[55] М. Dančo, M. Hnatič, M. V. Komarova, T. Lučivjanský, M. Yu. Nalimov, Phys. Rev. E 93 (2016) 012109
[56] M. Dančo, M. Hnatič, T. Lučivjanský, L. Mižišin, Phys. Rev. E 102(2) (2020) 02211
[57] Yu. A. Zhavoronkov, M. V. Komarova, Yu. G. Molotkov, M. Yu. Nalimov, J. Honkonen, Theor. Math. Phys. 169 (2019) 1237
[58] J. Honkonen, M. V. Komarova, Yu. G. Molotkov, M. Yu. Nalimov, Theor. Math. Phys. 200 (2019) 1360




