Deep learning for simulation and analysis of fine structure properties
Publications, 13 May 2022
We offer to your attention an article “Simulation and Analysis of Fine Structure Properties in Mass Distributions of Nuclear Reaction Products by Deep Learning Methods” published in the JINR News bulletin. The authors are G. A. Ososkov, Yu. V. Pyatkov, M. O. Rudenko.
One of the informative theoretical descriptions of nuclear reactions, such as fission and quasi-fission, presents the evolution of a nuclear system in the form of trajectories in a multidimensional deformation space. Finding images of such trajectories in the space of experimentally observable variables was proposed in [1, 2] as a new approach to data analysis. The trajectories look like “fine structures” in two-dimensional distributions, for example, in correlation mass distributions. By definition, fine structure means local regions (peaks) in a two-dimensional distribution with the yield higher than on a smooth substrate, which is the background to the sought-after effect. Sometimes experimental conditions make it possible to observe a trajectory almost without noise (background). In this case, the trajectory looks as a continuous sequence of points close, for example, to a straight line. In any case the trajectory revealed gives evidence of a strong correlation between the parameters of the reaction products. A correlation between the parameters of the nuclear system throughout the whole available phase space provides unique information about the mechanism of the process compared to mean values or variances often used. It wasthe revelation of the fine structure in the correlation mass distributions of fission fragments of low excited nuclei that allowed scientists of the Flerov Laboratory of Nuclear Reactions to observe for the first time a new type of the decay called collinear cluster tri-partition (CCT) [3,4]. This is a rather rare decay mode for the heavy actinides such as 252Cf(sf), but it can be very likely for the superheavies [5]. The correlated mass distributions of fission fragments from the spontaneous fission of californium 252Cf(sf) are shown in figure (experimental details are given in [6]).
Mathematicians of the Meshcheryakov Laboratory of Information Technologies were tasked with identifying the linear structure in the available experimental material and assessing the level of its validity in relation to the alternative hypothesis that in fact only a random sequence of points is observed. The uniqueness of this problem was determined by the fact that the experimental material was represented by a single two-dimensional distribution obtained in a very costly experiment [6], which could not be reproduced repeatedly to accumulate the necessary statistics. Nevertheless, the complex rhombo-helical form of the observed thin structure, called by physicists the “nuclear rose”, and a sufficient number of points, its constituents, enabled one to carry out its detailed statistical analysis and establish its following properties.
- The structure has the form of a rhombic meander, representing a family of 10 straight lines (M1+M2≈const). At their intersections there are points, the coordinates of which are close to the masses of the known magic nuclei [6], shown in figure.
- The meander points are uniformly distributed along the segments, and their number on each of the segments has a Poisson distribution with the parameter λ. Assuming that this parameter is common to all meander segments, it was estimated by the Kolmogorov criterion as λ=4.5.
- Assuming that the scatter of points around the segments is the same for all segments and subject to the normal law with parameters (0, σ), the parameter σ was also estimated by the χ2 criterion as σ=0.2.
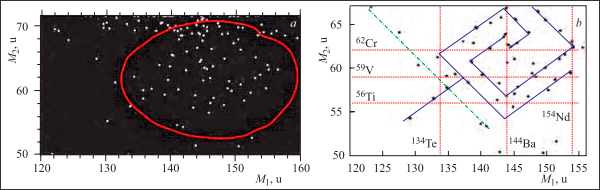 Correlation mass distribution of the 252Cf(sf) fission fragments: a) the specific rhombo-helical structure marked with an oval; b) the same structure on a larger scale. The blue lines drawn across the experimental points contribute to the visual perception of the structure. The red dotted lines indicate the masses of the magic nuclei [8]
Correlation mass distribution of the 252Cf(sf) fission fragments: a) the specific rhombo-helical structure marked with an oval; b) the same structure on a larger scale. The blue lines drawn across the experimental points contribute to the visual perception of the structure. The red dotted lines indicate the masses of the magic nuclei [8]
The combination of these properties made it possible to develop a numerical model of a fine structure, allowing the creation of independent images of similar structures with the same statistical properties.
To assess the reliability of the model of the fine structure with respect to the alternative hypothesis that this structure is a set of randomly scattered points, it was proposed:
- to create an image generator and generate images of two different types: images with a fine structure and images with randomly scattered points in the same field;
- to develop a neural classifier based on a deep convolutional neural network and train it on a dataset of the generated images to reliably recognise the image type.
The Python programming language with connected libraries, such as matplotlib, keras, tensorflow, scikit-learn, numpy, pandas [7], was used in the solution process. Next, a numerical experiment was carried out, and as a result, the probability of detecting a rhombic meander was obtained on an array of 105 statistically independent sets of random points using a deep neuroclassifier. This probability was negligibly small (0.017%), while the probability of the presence of a rhombo-spiral structure in the original image (figure) was 99.91%. We also obtained answers to two other questions of interest when planning similar experiments, namely, about an objective estimate of the range in terms of the noisiness of the distribution by background points, and about the limit of degradation of the spectrometer mass resolution, which allows us to isolate the desired structure at an acceptable level of reliability.
References:
[1] Pyatkov Yu.V. et al. // Pattern Recogn. Image Anal. 2011. V.21. P.82–87.
[2] Pyatkov Yu.V. et al. // Eur. Phys. J. A. 2012. V.48. P.94.
[3] Pyatkov Yu.V. et al. // Phys. Rev. C. 2017. V.96, No. 6. P.064606.
[4] Oertzen W. von, Nasirov A.K. // Eur. Phys. J. A. 2020. V.56. P.80.
[5] Balasubramaniam M. et al. // Phys. Rev. C. 2016. V. 93. P.014601.
[6] Pyatkov Yu.V. et al. eLIBRARY ID: 41346520. 2018. P. 285‒290.
[7] Top 10 Python Libraries for Data Science (in Russian).
[8] Ososkov G.A., PyatkovYu.V., Rudenko M.O. // Part. Nucl., Lett. 2021. V.18, No. 5 (237). P.430‒447 (in Russian).